Решите алгбера 8 класс
тема «дробные рациональные уравнения»
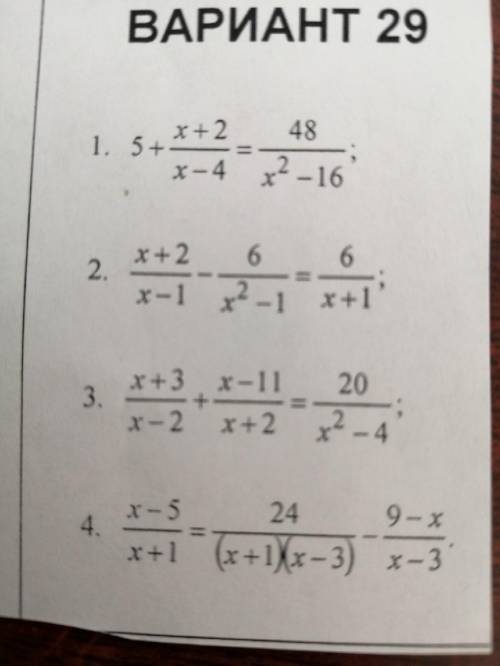

Другие вопросы по теме Математика
Популярные вопросы
- (1/2)`3*(3 1/3-2 8/9)`2 - это степень...
3 - Іть, будь ласка! скласти твір на тему жорстокість у суспільстві. як з...
2 - 1) как зависит сила тока от напряжения? почему? 2) почему вольтамперная...
3 - Составь слово из букв т н и н е р т е...
3 - Какое число является значением выражения [tex] \frac{ \sqrt{98} }{7}...
1 - 50 радиус колеса составляет 5 см. рассчитайте длину угла арки в 18 градусов...
1 - (a-5)^2+2(5-a)+1 x^6-x^4-x^2+1 желательно с объяснением...
1 - Опешите строение частиц sb h3 sb h4 методом вяленых связей: тип гибридизации...
2 - Известно что 3 юбки две блузки пиджак стоят 9600 руб 2 юбки и 4 блузки...
2 - Составить 4 предложения на все случаи слитного и раздельного написания...
1
Дано:
(1/x) + (1/(x+4)) = 5/12
Шаг 1: Умножим оба члена уравнения на наименьшее общее кратное знаменателей, чтобы избавиться от дробей. В данном случае, знаменатели - это x и (x+4), поэтому их наименьшее общее кратное будет x(x+4).
Теперь, умножим оба члена уравнения на x(x+4):
(x(x+4) * (1/x)) + (x(x+4) * (1/(x+4))) = (x(x+4) * 5/12)
В итоге получим:
(x+4) + x = 5(x(x+4))/12
Шаг 2: Распространим скобки и упростим уравнение:
x + 4 + x = (5x(x+4))/12
2x + 4 = (5x^2 + 20x)/12
Шаг 3: Умножим обе части уравнения на 12, чтобы избавиться от знаменателя:
12(2x + 4) = 5x^2 + 20x
24x + 48 = 5x^2 + 20x
Шаг 4: Перенесем все члены уравнения на одну сторону, чтобы получить квадратное уравнение:
5x^2 + 20x - 24x - 48 = 0
5x^2 - 4x - 48 = 0
Шаг 5: Теперь остается только решить полученное квадратное уравнение. Можно использовать метод факторизации, метод декремента или использовать квадратную формулу. В данном случае, решим уравнение, используя квадратную формулу, чтобы упростить объяснение:
Вспомним, что для квадратного уравнения вида ax^2 + bx + c = 0, корни можно найти с помощью формулы x = (-b ± √(b^2 - 4ac))/(2a).
В нашем случае:
a = 5, b = -4 и c = -48
Применим формулу:
x = (-(-4) ± √((-4)^2 - 4*5*(-48)))/(2*5)
x = (4 ± √(16 + 960))/10
x = (4 ± √976)/10
Шаг 6: Продолжим упрощение:
x = (4 ± √(16*61))/10
x = (4 ± 4√61)/10
x = (2 ± 2√61)/5
Таким образом, мы получили два возможных значения x: (2 + 2√61)/5 и (2 - 2√61)/5.
Это и есть итоговые решения данного уравнения.
Итак, решение уравнения (1/x) + (1/(x+4)) = 5/12 в общем виде: x = (2 + 2√61)/5 и x = (2 - 2√61)/5.
Надеюсь, это подробное решение помогло вам понять процесс решения дробного рационального уравнения. Если у вас есть еще вопросы, не стесняйтесь задавать их! Я всегда готов помочь.