решить задания по математике желательно с объяснениями и развернутыми ответами.. УСЛОВИЯ:
Для предоставленных матриц вычислить
а)
б) Если Е-единичная матрица,
в) ,
3. Решить систему линейных алгебраических уравнений:
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы.
4. Решить систему линейных алгебраических уравнений методом Жордана-Гаусса. Указать, сколько решений имеет система.
ИИ. Векторная алгебра
5. Для предоставленных в пространстве точек , , , :
а) найти координаты и модули векторов ;
б) найти единичный вектор,который является ортом вектора ;
в) найти внутренние углы треугольника, которые построены на векторах и ;
г) найти площадь треугольника, которые построены на векторах и ;
д) найти объем пирамиды, которые построено на векторах , и ;
е) определить, являются ли векторы, компланарными, а также попарно-неарными, перпендикулярными.
III. Аналитическая геометрия в пространстве
6. Для предоставленных в пространстве точек :
а) составить уравнение плоскости проходящей через точку ... которое перпендикулярна вектору ;
б) составить уравнение плоскости , проходящей через точки ;
в) определить угол между плоскостями И.
7. Для предоставленных в пространстве точек :
а) составить уравнение прямой , проходящей через точки... ;
б) составить уравнение прямой , проходящей через точки... ;
в) вычислить угол между прямыми
8. Для предоставленных в пространстве точек :
а) составить параметрические уравнения прямой , проходящей через точку
и является перпендикулярной к плоскости из задачи 6;
б) определить координаты точки пересечения прямой с плоскостью из задачи 6.
VI. Аналитическая геометрия на плоскости
9. Для предоставленных на плоскости точек :
а) составить уравнение медианы треугольника , проведенной к стороне ;
б) составить уравнение высоты треугольника , которая проведена из вершины , и определить ее длину.
10. Для уравнения кривой второго порядка , где – координати точки , выполнить:
а) привести уравнение кривой второго порядка к каноническому виду;
б) определить тип, найти координаты вершин и фокусов, эксцентриситет кривой.
в) изобразить кривую схематично на рисунке.
V. теория границ, непрерывность функции
11. Вычислить пределы с свойств бесконечно малых и не-конечно больших величин.
12. Вычислить пределы с теорем о пределах.
13. Вычислить пределы с стандартной границы.
14. Вычислить пределы с стандартной границы.
15. Исследовать функцию на непрерывность в точках и . Построить график функции.
VI. Производная функции и ее применение
16. Составить уравнения касательной и нормали к графику функции в точке .
17. Найти первую производную для предоставленных функций.
18. Вычислить дифференциал первого порядка для предоставленной функции.
19. Найти вторую производную функции и вычислить ее значение в данной точке.
вот я через переводчик перевел и исправил где недословно
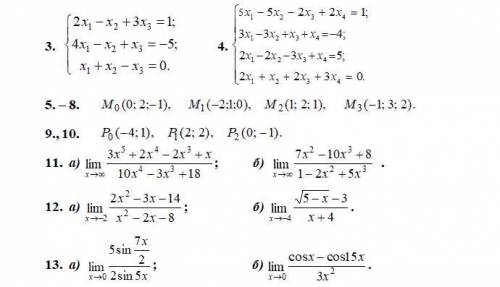

Ответы
Показать ответы (3)
Другие вопросы по теме Математика
Популярные вопросы
- X Хто перепише цей текст без помилок за 30хв тому ві (кто напишет єтот текст...
3 - 1)күрделі етістіктерді теріп жаз 2)Тегістеді,көңілді деген етістіктерді сөз құрамына...
1 - Дано:R1=20м R2=30м R3=40м R4=10м.Знайти:Rзаг ...
3 - Триатлон - мультиспортивная гонка, состоящая из непрерывного последовательного...
3 - До іть будь ласка швидко кр...
1 - Часи правління Іоанна Безземельного; Філіпа ІV; Оттона І...
3 - Әңгіме мазмұна сүйеніп,Тортайға міңездеме беріндер.Тортай тағдыры туралы эссе...
2 - Опишите фотографию, 5-7 предложений...
2 - Примеры стр 47 тренажёр яценко...
3 - Ребят сосчитайте 2 целых минус 9 восьмых ...
1