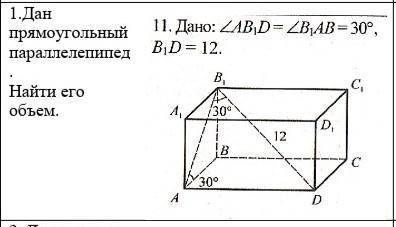
Математика: решить задачу по геометрии

решить задачу по геометрии

Ответы

nabiullinnazim 13.08.2020 08:28

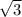ответ: (81* $\sqrt{3}$ )/2

Пошаговое объяснение:

Очевидно, Δ AB₁D - прямоугольный, ∠ B₁AD = 90° отсюда, с учетом

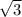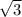∠ AB₁D = 30° имеем: AD=¹/₂ * BD=6, AB₁= $\sqrt{3}$ /2 * BD = 3 $\sqrt{3}$ ,

далее Δ AB₁B - прямоугольный, отсюда, с учетом

∠ BAB₁ = 30° имеем: BB₁=¹/₂ * AB₁ =3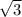 $\sqrt{3}$ /2, AB= 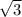$\sqrt{3}$ /2 * AB₁ = 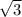$\sqrt{3}$ /2 * 3 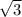$\sqrt{3}$ =9/2

Объем: BB₁*AB*AD=3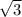 $\sqrt{3}$ /2 * 9/2 * 6=3 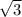$\sqrt{3}$ /2 * 27= 81 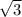$\sqrt{3}$ /2

ПОКАЗАТЬ ОТВЕТЫ

larakav 15.01.2024 22:48

Чтобы решить данную задачу по геометрии, нужно использовать основные свойства треугольника и лишь немного алгебры.

Итак, у нас есть треугольник ABC. Известно, что угол ABC равен 60 градусов, а сторона AC равна 4 единицы.

Чтобы решить задачу, мы сначала найдем длину стороны AB, используя теорему косинусов. Данная теорема выглядит следующим образом:

c^2 = a^2 + b^2 - 2ab*cos(C),

где c - сторона напротив угла C, a и b - остальные две стороны, C - угол, напротив которого находится сторона c.

В нашем случае, стороны a и b равны 4 единицы (сторона AC) и x единиц (сторона AB) соответственно, а угол C равен 60 градусов.

Подставим известные значения в формулу:

x^2 = 4^2 + x^2 - 2*4*x*cos(60°).

Далее, упростим выражение:

x^2 = 16 + x^2 - 8x*cos(60°).

Можем заметить, что в упрощенном выражении есть косинус 60 градусов. Известно, что косинус этого угла равен 1/2. Подставим это значение в формулу:

x^2 = 16 + x^2 - 8x*(1/2).

x^2 = 16 + x^2 - 4x.

Далее, перенесем все x-термы на одну сторону уравнения, а числовые константы на другую:

x^2 - x^2 + 4x = 16.

4x = 16.

Теперь разделим обе части уравнения на 4:

x = 16/4.

x = 4.

Таким образом, мы получили, что сторона AB равна 4 единицы.

Ответ: сторона AB равна 4 единицы.

На картинке, где дана геометрическая фигура, сторона AB обозначена буквой "х". На основе наших вычислений мы установили, что "х" равно 4 единицы.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика