Решить задачу Коши
Заранье
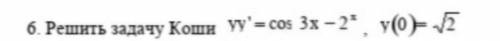
Другие вопросы по теме Математика
Популярные вопросы
- 1. раскройте скобки, употребляя глаголы в требующемся времени. 1. i (to call) tom...
1 - Панда аюлар тобына жататын жануардың түрі. ол өте сүйкімді.оның денесі де ерекше....
1 - A=-2i+j,b[10; -15],c=3a-1/5b найдите кординаты точки c...
1 - Что такое спаредливый лидер государства пример...
3 - Как изменились материки за много лет...
2 - Чему равна плотность жидкости , 130 л. которой имеют массу 120 кг?...
1 - Нужно сочинение по произведению д. а. фонцивина недоросль на тему: проблемы воспитания...
2 - Какие виды жестокого обращения с детьми вы знаете?...
2 - Длина кирпича 25 см ширина 120 мм толщина 60 мм определите плотность если его масса...
3 - Железнодорожный вагон массой m движущийся со скоростью сталкиваетсч с неподвижным...
2
частное решение
общее решение