Решить задачу Коши по математике
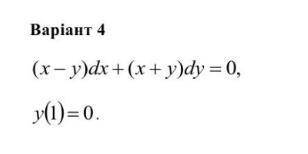
Другие вопросы по теме Математика
Популярные вопросы
- Определи, с какой скоростью должен ехать мотоцикл, чтобы пройти 45 км за...
2 - 8 класс Раздел 2. Искусство белорусских земель в Средневековье(задания...
1 - решить, номер 12.3 кроме 1 и 4...
3 - Поставить точку и от неё провести линии по следующим азимутам 90* 180*...
2 - Ріка що протікає через Болгарію на березі якої Святослав хотів княжити?...
3 - 1. Present perfect simple tense in Russian? 2. Вс глагол в present perfect...
2 - Наименьшее общее кратное и 12,4 и наименьший общий делитель 12,4...
3 - Прочитайте текст и выполните задания: (1) Хороши русские снежные зимы!...
3 - решить задачу! Какой вместимости надо взять сосуд, чтобы в него можно было...
3 - Самый древний источник тепловой энергии на Земле , 9 букв даю 15...
2
Однородное ДУ
общее решение
частное решение