1. Математика
  2. Решить задачу коши для системы

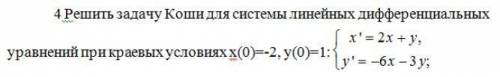
Решить задачу коши для системы линейных дифференциальных уравнений


Решить задачу коши для системы линейных дифференциальных уравнений

ayvazyanloxq37n ayvazyanloxq37n    3   08.06.2020 15:32    0

Ответы
vmatveicheva vmatveicheva  15.10.2020 13:25

Пошаговое объяснение: Решать будем с преобразования Лапласа. Т.е. будем находить изображение функции (оригинала). При этом будем пользоваться теоремой о дифференцировании

\[f^n (t) = p^n F(p) - \sum\limits_{k = 0}^{n - 1} {p^{n - 1 - k} f^k (0)} \]

Тогда производные x' и y' будут иметь вид

\[\begin{array}{l} x' = pX(p) - x(0) \\ y' = pY(p) - y(0) \\ \end{array}\]

Получаем систему уравнений (учитывая теорему о линейности)

\[\left\{ \begin{array}{l} pX(p) - x(0) = 2X(p) + Y(p) \\ pY(p) - y(0) = - 6X(p) - 3Y(p) \\ \end{array} \right.\]

Начальные условия x(0) и y(0) нам известны, поэтому не трудно будет решить данную НСЛДУ

\[\left\{ \begin{array}{l} X(p) = \frac{{2Y(p) + x_0 }}{{p - 2}} \\ Y(p) = \frac{{y(0) - 6X(p)}}{{p + 3}} \\ \end{array} \right. \Rightarrow Y(p) = \frac{{1 - 6\left[ {\frac{{2Y(p) + x_0 }}{{p - 2}}} \right]}}{{p + 3}} = \frac{{p - 2 - 12Y(p) + 12}}{{\left( {p - 2} \right)\left( {p + 3} \right)}}\]

Последний шаг - с метода неопределенных коэффициентов разбить на простейшие дроби и закончить задачу с обратного преобразования Лапласа.

Удачи!)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
zmey7755 zmey7755  18.07.2019 13:10
Найдите сумму корней уравнения 7(4-х/7) в квадрате =3(х/7-4)...
nastycherry1 nastycherry1  18.07.2019 13:10
Как решить андрей прочитал повесть за два дня .в 1 день он прочитал 18 страниц.это на 10 страниц меньше ,чем он прочитал во 2 день.сколько страниц в повести...
Olgarezkova Olgarezkova  18.07.2019 13:10
Три сестры оля,ира и маша пили вместе чай. ира+оля-выпили 11 чашек. ира+ маша- выпили 15 чашек. оля+ маша - выпили 14 чашек. сколько чашек чая выпито всего?...
Brauberg898117 Brauberg898117  18.07.2019 13:10
Коля на 3 года старше вани и на 4 года младше юрий. на сколько лет юра старше вани...
VeryLittleTasia VeryLittleTasia  18.07.2019 13:10
Вуравнении неизвестное обозначено буквой х, число 1 является корнем уравнения (7x-a)+a=1-2x. найдите, какое число обозначено при этом буквой а...
ivanvlasuyk80 ivanvlasuyk80  18.07.2019 13:10
Туристи вирушили у триденний похід.за перший день вони пройшли 3/11,а за другий -4/11усього шляху.скільки кілометрів пройшли туристи за третій день, якщо весь маршрут становивв44 км....
nn814921 nn814921  18.07.2019 13:10
Поясніть, чьому для підлітків важливе самопізнання если не знаешь, не пиши!...
mariarura mariarura  18.07.2019 13:10
Андрей прочитал повесть за 2 дня в первый день он прочитал 18 страниц это на 10 меньше чем он прочитал во второй день сколько страниц в повести...
Violetta291 Violetta291  18.07.2019 13:10
Автомобиль проехал 8/13 намеченного маршрута . какова общая длина маршрута , если автомобиль проехал 120 км...
Skvaler Skvaler  18.07.2019 13:10
Найти длину окружности если ее радиус равен 35 дм. число п округлить до десятых...

Популярные вопросы