Решить задачу коши для дифференциального уравнения первого порядка с разделяющимися переменными
1)y'-1=e^x ; x=0; y=1
2)y'+8x^3y=0; x=0; y=5
Другие вопросы по теме Математика
Популярные вопросы
- Запишите решение если к задуманному числу прибавить 37 а потом...
3 - Определите стихотворный ! мороз и солнце; день чудесный! еще ты...
2 - Саламандра и ящерица эти два животных внешне похожи...
1 - Подобные слагаемые а)3х+ 5х-х= б) 9 y -6х+ х= в)х-5х+9х= г)14а+а-15а=...
3 - Природные условия в египте и россии...
3 - Какие семьи бывают чем отличается двухпоколенная семья 3 поколения...
1 - Составить бизнес план по плану: 1)мой собственный бизнес 2)затраты...
2 - Вразных формах слова чеснок выделить окончание. для чего служит...
1 - 1. возникновение письменности относится к : а) 1 веку до н.э....
2 - 100 слов о христофоре колумба что он совершил и (или) как. заранее...
2
1)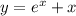
2)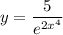
Пошаговое объяснение:
1)
Интегрируем правую и левую часть
Решаем задачу Коши:x=0; y=1
ОТВЕТ
2)
(А не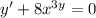 так как это не дифференциальное уравнение первого порядка с разделяющимися переменными)
так как это не дифференциальное уравнение первого порядка с разделяющимися переменными)
Интегрируем правую и левую часть
Для удобства пишем свободный член lnC
Экспоненцируем
Решаем задачу Коши:x=0; y=5
ОТВЕТ