... Решить задачу коши...
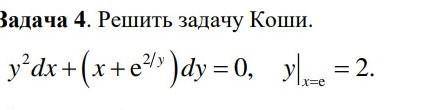
Другие вопросы по теме Математика
Популярные вопросы
- Система неравенств , решите и укажите целые числа 2х-3 3x+5 5x+2...
1 - Решить ! расстояние между александровкой и бекасово 4 км. 500 м. из александровки...
1 - Про числа а и b известно, что а b.из следующих неравенств выберите верное: 1)...
2 - Почему магнитные и полюса замли не ?...
3 - Подумай что обозначают эти слова и запиши синонимы к ним хищное ассортимент хребет...
1 - Посоветуйте что можно сделать из дерева (7 класс)...
1 - (7y-2)(во второй степени)+25y=1+49y(вторая степень)...
1 - Просклоняйте по падежам словосочетание полтора дня...
2 - Ккакой группе животных относится страус?...
3 - Нужно сочинение миниатюра 10 ! заранее огромное ыονρζ...
2
ответ: y=2/ln(x).
Пошаговое объяснение:
Перепишем уравнение в виде dx/dy+x/y²+e^(2/y)/y²=0 и будем искать решение в виде x=x(y). Это - ЛДУ 1 порядка относительно x, полагаем x=u*v. Тогда dx/dy=x'=u'*v+u*v' и уравнение принимает вид: u'*v+u*v'+u*v/y²+e^(2/y)/y²=0, или v*(u'+u/y²)+u*v'+e^(2/y)/y²=0. так как одну из функций u или v мы можем выбрать произвольно, то поступим так с u и потребуем, чтобы она удовлетворяла уравнению u'+u/y²=0. решая его, находим u=e^(1/y). Тогда уравнение принимает вид: e^(1/y)*v+e^(2/y)/y²=0, или v'=-e^(1/y)/y². Заменяя v' на dv/dy и учитывая, что -dy/y²=d(1/y), перепишем это уравнение в виде: dv=e^(1/y)*d(1/y). Интегрируя, находим: v=e^(1/y)+C, где C - произвольная постоянная. Тогда x=u*v=e^(2/y)+C*e^(1/y). Используя условие y(e)=2, приходим к уравнению e=e+C*e^(1/2). Отсюда C=0 и тогда искомое частное решение x=e^(2/y), а тогда y=2/ln(x).