Другие вопросы по теме Математика
aminibragimov05
27.05.2020 18:12
iuhagng
27.05.2020 18:12
daryaevis
26.05.2020 17:38
НастюшКа50471
26.05.2020 17:38
Filomena0w0
27.05.2020 18:12
Sasha34634
27.05.2020 06:05
nafasomf188
27.05.2020 18:12
makhero111
27.05.2020 18:12
Популярные вопросы
- Рассчитать развлетвленную цепь...
2 - Вряд вбиты 20 гвоздей, каждый из которых торчит на 10 сантиметров. плотник по...
2 - робинзон крузо навивки приобретённые на острове?...
3 - Объясните подробно как это сделали! ...
3 - Проволоки длиной 6 м отрезали сначала 3,4 м а затем еще две пятых сколько метров...
1 - Прочитайте. напишите сочинение об этом рассказе, отвечая на поставленные вопросы....
1 - Найдите и исправьте ошибку (ошибки) в образовании формы слова. запишите правильный...
1 - Wolfram mathematica нужно написать программку , которая будет выполнять данные...
3 - Таблица 8.3 свойства параллели параллелограмма ...
2 - Решить смешанные и дробные числа 1) (5.1/2*8)*(2/3*12)-3.3/5*5= 2) 4.2/3+7/15*1.1/5=...
3
sqrt(2)
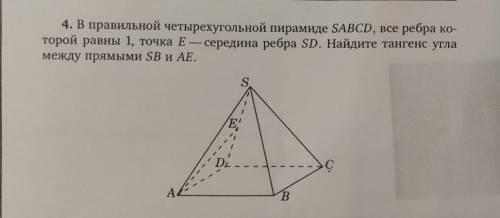
Пошаговое объяснение: Пусть М -середина DB.
MЕ||SB и MЕ=0,5 (средняя линия в треугольнике DBS). MЕ=0,5 AЕ=sqrt(3)/2 (высота в равностороннем треугольнике) AM=sqrt(2)/2 (половина диагонали квадрата)
AЕ^2=MЕ^2+AЕ^2. Значит треугольник МАЕ - прямоугольный. Угол ЕМА - прямой. Тангенс угла АЕМ равен АМ/ЕМ=sqrt(2). Так как MЕ||SB, тангенс равен искомому.
sqrt - корень квадратный