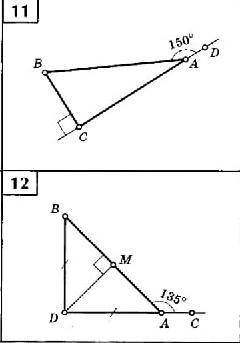
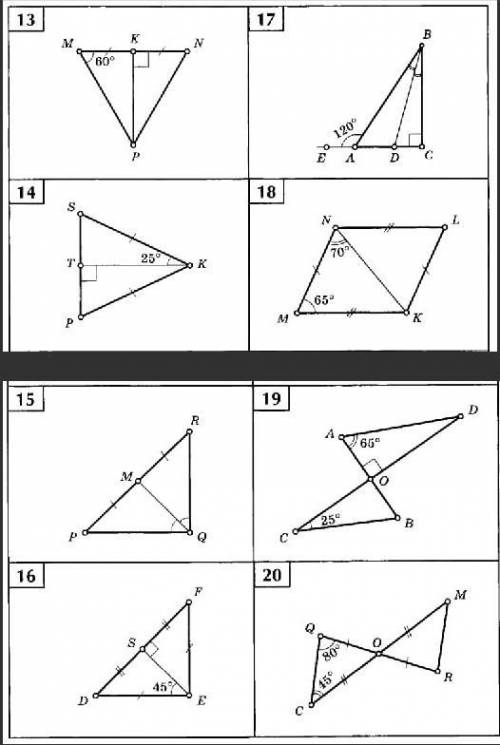
решить задачи по геометрии. Запишите только ответ

Давайте по очереди рассмотрим каждую задачу.

Задача 1:
В задаче двум пунктам требуется найти площади различных фигур.

a) Первое, что мы видим, это равнобедренный треугольник ABC, у которого стороной AC обозначена диагональ квадрата. Если диагональ квадрата является основанием равнобедренного треугольника, то высота этого треугольника будет перпендикулярна к основанию и проходить через его вершину (т.е. точку A). Таким образом, мы можем заметить, что треугольник ABC может быть разделен на два прямоугольных треугольника с высотами AC и BC соответственно.

Так как мы знаем, что диагональ квадрата равна 12 см, можно сказать, что сторона квадрата равна 12/√2, так как диагональ квадрата является гипотенузой одного из треугольников. Таким образом, получается, что высотой прямоугольного треугольника является сторона квадрата, то есть 12/√2.

Формула для площади прямоугольного треугольника:
Площадь = (основание * высота) / 2

Providing the given values into the formula:
Площадь = (12/√2 * 12/√2) / 2
= (144/2) / 2
= 72 / 2
= 36

Ответ: Площадь равнобедренного треугольника ABC равна 36 квадратным сантиметрам.

b) Другая фигура, которую нужно рассмотреть, это прямоугольник ADEH. Мы видим, что эта фигура делится на два прямоугольника по диагонали AC.

Обратите внимание, что эти два прямоугольника являются прямоугольными треугольниками, так как их углы прямые. Давайте найдем площадь каждого треугольника по формуле:
Площадь = (основание * высота) / 2

Для прямоугольника ABDG:
Площадь = (ширина * высота) / 2
= (6 * 8) / 2
= 48 / 2
= 24

Для прямоугольника CDFG:
Площадь = (ширина * высота) / 2
= (6 * 10) / 2
= 60 / 2
= 30

Теперь мы можем найти площадь всего прямоугольника ADEH, сложив площади двух треугольников:
Площадь = Площадь ABDG + Площадь CDFG
= 24 + 30
= 54

Ответ: Площадь прямоугольника ADEH равна 54 квадратным сантиметрам.

Задача 2:
В этой задаче требуется найти общую площадь цветных частей фигуры.

Для этого нам нужно найти площадь каждого из трех секторов круга и сложить их. Зная, что сумма всех углов в круге равна 360 градусов, и что цветная часть занимает 160 градусов, мы можем найти площадь цветной части.

Формула для площади сектора круга:
Площадь = (угол / 360) * площадь круга

Providing the given values into the formula:
Площадь сектора 1 = (80 / 360) * π * (3^2)
= (2 / 9) * 9π
= 2π

Площадь сектора 2 = (40 / 360) * π * (3^2)
= (1 / 9) * 9π
= π

Площадь сектора 3 = (40 / 360) * π * (3^2)
= (1 / 9) * 9π
= π

Теперь сложим площади всех трех секторов:
Площадь = Площадь сектора 1 + Площадь сектора 2 + Площадь сектора 3
= 2π + π + π
= 4π

Ответ: Общая площадь цветных частей фигуры равна 4π квадратным единицам.

Надеюсь, что объяснение было понятным для вас, и вы получили нужные ответы. Если у вас возникли еще вопросы, пожалуйста, не стесняйтесь задать их.