РЕШИТЬ. Я НЕ ШУЧУ, МЕНЯ ИЗБИВАЮТ ЗА ЭТО... СИСТЕМА УРАВНЕНИЙ
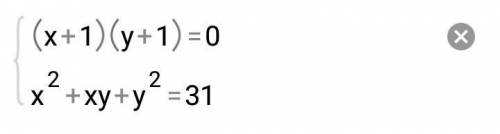
Другие вопросы по теме Математика
Популярные вопросы
- 14×2 11/14 решите пример с решением...
2 - 30 ! что подтверждает мощь папы римского?...
2 - Вычислить площадь фигуры ,ограниченной линиями: y=x^2+1; y=2x+9; x=0;...
3 - Must the children work for having money?...
3 - Сочинение капитанская дочка . план: 1. честь и долг проявляется в жизненных...
1 - 7класс дано : v=3л p (ро) - 1030 кг/м3 (кубический) m - ?...
1 - Дано abc прямоугольный треугольник угол b равен 36,угол c равен 90°.найдите...
1 - Какой металл встречается в земной коре только в виде соединений...
2 - Задайте формулой прямую пропорциональность, график которой параллелен...
1 - Серик может съесть коробку конфет за 12 минут, а берик такую же коробку...
3
{ (x+1)(y+1)=0
{ x²+xy+y²=31
Если произведение равно нулю, то хотя бы один из множителей равен нулю, то есть
(x+1)(y+1)=0
х+1=0 у+1=0
х₁= -1 у₂= -1
Подставим х₁ во второе уравнение системы
(-1)²+(-1)y+y²=31
1-y+y²=31
y²+1-y-31=0
y²-y-30=0
{ у₁₁+у₁₂= 1
{ у₁₁*у₁₂= -30
у₁₁= 6 у₁₂= -5
Здесь мы получили такие решения: (-1; 6) и (-1; -5)
Теперь подставляем у₂= -1 во второе уравнение системы
x²+x*(-1)+(-1)²=31
x²-x+1=31
х²-х-30=0
{ х₂₁+х₂₂= 1
{ х₂₁*х₂₂= -30
х₂₁= 6 х₂₂= -5
Здесь получили (6; -1) и (-5; -1)
Объединяем полученные решения
ответ: (-1; 6) ; (-1; -5) ; (6; -1) ; (-5; -1)