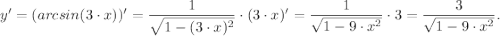Решить y=arcsin 3x (найти производную функции)
Другие вопросы по теме Математика
Популярные вопросы
- Как определить форму времени и глагола?...
1 - Скільки часу падало тіло без початкової швидкості,якщо за останні часи 2 с...
2 - Рассчитайте массу сульфата цинка содержащую 1,99*10^25 электронов. расчищайте...
3 - Эссе на тему доведіть або спростуйте думку про те чи кожен може й повинен...
1 - 1) колорит и национальный характер . карамзин наталья боярская дочь 2) тарас...
3 - Ть скільки важить в гасі алюмінієва деталь масою 270 г? густина гасу 800 кг/м3...
1 - Перепишите следующие предложения; подчеркните в каждом из них глагол-сказуемое...
1 - Морфологический разбор слова открывающегося...
2 - Abc-триуголник( прямоугольный 90градус)угол с=90 градуссd- биссектрисаac=3bc=4найти:...
3 - По тексту составить 5 вопросов,кто шарит в казахском...
2
Пошаговое объяснение:
Производная от сложной функции y=f(g(x)):
y'=f '(g(x))·g'(x).
По таблице производных:
Дана функция y=arcsin(3·x). Вычислим производную как от сложной функции: