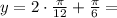решить
Вычислите определенный интеграл
Другие вопросы по теме Математика
Популярные вопросы
- МНЕ ЭТО ОТПРАВЛЯТЬ ЗАВТРА Я НЕ ЗНАЮ КАК ЭТО РЕШИТЬ!...
1 - (Складання рівнянь реакцій) Al(OH)3 + NaOH = HBr + Cu(OH)2 =FeCl3 + Ba(OH)2 = MgO...
1 - Створити асоціативний ряд до слова «Доля». Навести приклади із життя, які підтверджують...
2 - Накресліть схеми складного речення 1. Острах що він під час блукання загубить свою...
3 - Кто был главой городского самоуправления в 17-том веке в Российском государстве?...
3 - Около куба с ребром √48 описан шар. Найдите площадь поверхности шара....
2 - Почему Москва стала центром объединения Русских земель? - Какие слои населения были...
2 - Найдите сумму пятнадцати первых членов арифметической прогрессии (аn), если а1+а5=24...
3 - У прямокутному трикутныку ABC з прямим кутом C гипотенуза AB доривнюе-25см, а катет...
2 - Чим були пов язані міста Кафа і Ясир?...
3
При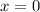 имеем
имеем 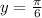 .
.
При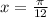 имеем
имеем