Решить все там где точкой отмечено. 50 ! заранее !
Другие вопросы по теме Математика
Популярные вопросы
- Допиши слова в соответсвующих формах.(просто строчная буква) 1.Columbus ___...
3 - Найдите значение выожение -а=2/5-3/8...
2 - В честь кого назван водопад Игуасу? (Отвечайте нормально) ...
1 - На множестве X={a, b, c, p} задано отношение R={(a, a), (b, b), (b, a), (c,...
3 - Выходной зимний день. Дети играются, спускаясь с горки на тюбингах. Радостно...
1 - Может ли площадь ортогональной проекции многоугольника быть большей площади...
2 - ВЫЧЕСЛИ И ЗДЕЛАЙ ПРОВЕРКУ 456 840:846...
1 - Part B Check (V) the one that suits the blank naturally. 1. Before Kimberly...
2 - С какими из перечисленных веществ будет реагировать соляная кислота: хром,...
3 - Определи, верны ли утверждения, ставя (+) в поле ввода. УтверждениеВерноНеверноГлобус...
3
1. 2cos4x - √2 = 0;
2cos4x = √2;
cos4x = √2/2;
4x = ±arccos(√2/2) + 2πn, n∈Z;
4x = ±π/4 + 2πn, n∈Z;
x = ±π/16 + πn/2, n∈Z;
2. cos(arcsin(-1/2) + arctg√3 + arccos(1/2)) = cos(-π/6 + π/3 + π/3) = cos(π/2) = 0.
Отже, cos(arcsin(-1/2) + arctg√3 + arccos(1/2)) = 0. Тотожність доведено.
3.
а) 2sin²x - 2cos²x = 1;
-2(cos²x - sin²x) = 1;
-2cos2x = 1;
cos2x = -1/2;
2x = ±arccos(-1/2) + 2πn, n∈Z;
2x = ±2π/3 + 2πn, n∈Z;
x = ±π/3 + πn, n∈Z.
б)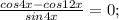 ОДЗ: sin4x ≠ 0
ОДЗ: sin4x ≠ 0
З врахуванням ОДЗ маємо:
4x=π/2 + πn, n∈Z;
x=π/8 + πn/2, n∈Z;