Решить в натуральных чисел. х^3-4х=у^2

Пусть числа x, y взаимно просты.

Поделим обе части на ;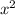

Получим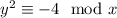 . Рассмотрим минимальное такое значение y.

Пусть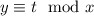 , причем 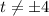. Тогда  

, но , противоречие.

Значит, .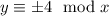

Пусть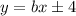 ; Получаем уравнение: 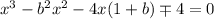, так как мы ищем натуральные решения, то они лежат среди натуральных делителей свободного члена. Проверяя, получаем, что решений в натуральных числах нет.