Решить уравнения а) корень из 3 tg2x=1, б) 2sin^2x+3cos=0, в) 6 sin^2x+5sinx+1=0, г) sin^2x+sinxcosx=0, д)2sinx-cos^2xsinx=0
Другие вопросы по теме Математика
Популярные вопросы
- Решить по теплоход км по течению реки и 42 км против течения реки,затратив на...
1 - Что значит жить по правилам? какие правила существуют в обществе? что такое права...
2 - Расскажите о древнейшей цивилизации индии...
2 - Распри в московском княжестве сообщение ( надо)...
3 - Найти наименьшее значение функции y=x^2+4x-3 на промежутке [0; 2]...
1 - Округлиье десятичную дробь: а) 239,52 до единиц; б) 34,346 до десятых; в)22,829...
1 - Подчеркните грамматическую основу и причастные обороты. хорошо работающая память...
1 - 1) солнце ,планеты и другие тела которые движутся вокруг :...
2 - Подобрать к пословице все мы живем на божьей росе,под крамным солнышком подобрать...
1 - Скакими из следующих веществ реагирует naoh - cr2o3, na2co3, ba(oh)3, no, p2o5,...
1
a)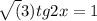
zamena-cosx=t
2-2t^2+3t=0
t1=-2
t2=1/2
решаем уравнение заменой
cosx=-2 решений нет
cosx=1/2
x=+-pi/3+2pi*n
в) 6sin^2x+5sinx+1=0
zamena sinx=t
6t^2+5t+1=0
t1=-1/2
t2=-1/3
sinx=-1/2
x=(-1)^(n+1)*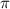 /6+
/6+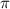 n
n
sinx=-1/3
x=(-1)^(n+1)*arcsin(1/3)*pi*n
г)sin^2x+sinxcosx=0
sinx(sinx+cosx)=0
sinx=0
x=pi* n
и
sinx+cosx=0
tgx+1=0
tgx=-1
x=-pi/4+pi*n
д)2sinx-cos^2xsinx=0
sinx(2-cos^2x)=0
sinx=0
x=pi*n
cos^2x=2
cosx=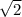
x=+-arccos(\sqrt2" alt="2sin^2x+3cosx=0" />
zamena-cosx=t
2-2t^2+3t=0
t1=-2
t2=1/2
решаем уравнение заменой
cosx=-2 решений нет
cosx=1/2
x=+-pi/3+2pi*n
в) 6sin^2x+5sinx+1=0
zamena sinx=t
6t^2+5t+1=0
t1=-1/2
t2=-1/3
sinx=-1/2
x=(-1)^(n+1)*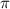 /6+
/6+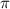 n
n
sinx=-1/3
x=(-1)^(n+1)*arcsin(1/3)*pi*n
г)sin^2x+sinxcosx=0
sinx(sinx+cosx)=0
sinx=0
x=pi* n
и
sinx+cosx=0
tgx+1=0
tgx=-1
x=-pi/4+pi*n
д)2sinx-cos^2xsinx=0
sinx(2-cos^2x)=0
sinx=0
x=pi*n
cos^2x=2
cosx=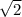
x=+-arccos(\sqrt2" />)+2pi*n