1. Математика
  2. Решить уравнениебез фотоматча​

Решить уравнение
без фотоматча​


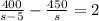
\frac{400}{s - 5} - \frac{450}{s} = 2

diana29012005 diana29012005    3   11.01.2021 13:24    0

Ответы
Arina001234hh Arina001234hh  10.02.2021 13:28

найдем наименьшее общее кратное

это

s(s - 5)

\frac{450}{s - 5} \times (s(s - 5)) - \frac{450}{s} \times (s(s - 5)) = 2 \times (s(s - 5)) \\

упростим

450s - 450(s - 5) = 2 \times (s(s - 5) \\ 450s - 450s - 450 \times - 5 = 2 \times (s(s - 5) \\ 450s - 450s + 2250 = 2(s(s - 5)) \\ 0 + 2250 = 2(s(s - 5)) \\ 2250 = 2(s(s - 5)) \\ 2250 = 2s {}^{2} - 10s

2s {}^{2} - 10s - 2250 = 0 \\ 2(s {}^{2} - 5s - 1125) = 0 \\ s {}^{2} - 5s - 1125 = 0 \\

найдем дискриминант

( - 5) {}^{2} - 4 \times (1 \times - 1125) \\ d = 181

s = \frac{5 + 5 \sqrt{181} }{2}

s = \frac{5 - 5 \sqrt{181} }{2}

ПОКАЗАТЬ ОТВЕТЫ
dashaloh000 dashaloh000  10.02.2021 13:28

Пошаговое объяснение:

Приведем к общему знаменателю:    s(s-5)

400s-450(s-5)=2s(s-5)

400s-450s+2250=2s²-10s.

2s²+40s-2250=

s²+20s-1125=0

s₁₂=-10±√1225=-10±35/

s₁=-10+35=25.

s₂=-10-35=-45.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
knyzeva2804 knyzeva2804  17.11.2020 23:02
Офисная мебель была куплена за 24000$. Норма амортизаци 15%. Какова будет стоимость после 2 года и...
Апрепр Апрепр  17.11.2020 23:03
Приведите пример такого квадратного трехчлена P(x), что при любом x справедливо равенствоP(x) + P(x + 1) + · · · + P(x + 10) =x^2 ​...
Znanija111tHtn Znanija111tHtn  17.11.2020 23:03
Відрізок А1В1-ПАРАЛЕЛЬНА ПРОЕКЦІЯ ВІДРІЗКА АВ на площини a .Знайдіть довжинувідрізка ММ1,якщо АА1||BB1||MM1,AM:MB=3:2 і AA1=14СМ,BB1=10СМ...
закро закро  17.11.2020 23:03
Розшифруй: 8 + = 8; 8- A= 8;+ 0 = 8.​...
еддпмаад еддпмаад  17.11.2020 23:03
нужно пешить задачу У діжку налили 32 л води і заповнили 4дробовариска7 об єму. Скільки л вміщається в діжку? ​...
ffffffffffffff52 ffffffffffffff52  16.08.2019 07:30
двое туристов направляются из пункта а в пункт в, расстояние между этими пунктами равно 60 км. у них есть один велосипед на двоих, ездить на нем вдвоем запрещено. велосипед допустимо...
Волщебница Волщебница  16.08.2019 07:30
Решите уравнение 2x+1/3=1/2 / это черта дроби / но не знак черта дроби /...
Ви2006ка Ви2006ка  16.08.2019 07:30
На месте вырубленных еловых лесов сначала чаще всего появляется березы,осины .почему? ?...
Fgbjhjghhy1234567890 Fgbjhjghhy1234567890  16.08.2019 07:30
Найдите площядь поверхности прямоугольного пароллелепида, измерения которого равны 9 м,24 м,11 м...
881881881 881881881  16.08.2019 07:30
Решите по действиям 1 пример 147-9-2 умножить 31+(94357-36792) делить 1985= решите...

Популярные вопросы