Решить уравнение: (x-6)^6+(x-4)^6=64

Рассмотрим функцию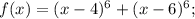 уравнение принимает вид f(x)=64. Исследуем функцию на монотонность с производной:

Найдем нули производной:

Подставив в производную x=4<5, убеждаемся, что она отрицательна, то есть функция слева от 5 убывает. Подставив в производную x=6>5, убеждаемся, что она положительна, то есть функция справа от 5 возрастает. Следовательно, слева от 5 уравнение имеет не больше одного решения, точно так же справа от 5 уравнение имеет не больше одного решения. Эти решения легко угадываются: x=4 и x=6.

ответ: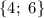

Замечание. Альтернативный решения - сделать замену x-5=t, после чего возвести (t-1) и (t+1) в шестую степень.