Решить уравнение (x^2-a^2)^2=4ax+1относительно x

Пусть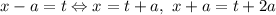

Сумма коэффициентов перед t равна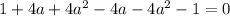 , значит, t = 1 — корень данного уравнения. Также заметим, что перед нечётными степенями t стоят противоположные коэффициенты, а остальные в сумме дают 0 — отсюда следует, что t = -1 также является корнем данного уравнения (при возведении t в чётную степень минус исчезает, а перед нечётными степенями t просто меняется знак, но так как они противоположны, они всё равно в сумме дадут 0).

Поделив левую и правую части на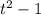 , получим уравнение:

Оно решений не имеет. Значит,

ответ: x = a±1

x = a±1

Пошаговое объяснение:

(x² - a²)²-4ax -1 =0 ⇔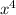 + 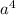-2a²x² -4ax -1 = 0 ⇔

+ + 2a²x² - ( 4a²x²+4ax +1) ⇔

(x²+a²)² - (2ax+1)² = 0 ⇔ ( x²+a²-2ax -1)·(x²+a²+2ax+1 ) = 0 ⇔

x²+a²-2ax -1 = 0  (1)  или x²+a²+2ax+1 =0 ( 2)

решим (1) :  x²+a²-2ax = 1 ⇔ (x-a)² = 1 ⇔ x - a = ±1  ⇔x = a± 1

решим (2) :  x²+a²+2ax = -1 ⇔ (x+a)² = - 1 ⇔ x∈∅

ответ : x = a± 1