Решить уравнение 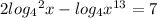 . В ответе указать наименьший корень уравнения
. В ответе указать наименьший корень уравнения
Другие вопросы по теме Математика
Популярные вопросы
- Основными причинами возникновения дюн и бархонов является...
2 - 9. Пушкин «Ескерткіш» өлеңінде өз шығармасының кейін басқа тілдерде тарайтынына...
2 - Ґрунтуючись на прочитаний за темою творах наведи приклади різних точок зору...
3 - 1. Укажите строку, в которой все наречия пишутся через дефис: а) (по)дружески,...
3 - Физика 8 класс решите что видно...
1 - мне пиз@ецПодготовьтесь к защите проектной работы: «Природа – бесценный дар»....
2 - Количество соединений 4:Цицерон Вергилий Гораций Овидий ,,Торжественная песнь...
2 - 3.Развернутый MON разделен лучом OF на два угла FOM и FON. Найдите градусные...
2 - 2 GRAMMAR comparative adjectives a Look at the adjectives in the quiz sentences.In...
3 - :11 1) 136 - ) (1-3) (10 - 970)2)(1+)2-1: (99 - 98);7 751773)23+455+221-1115:...
3
Заменяем log4(x) на t:
Делаем обратную замену:
Самый наименьший корень 1/2
ответ : 1/2