Решить уравнение, указать корни уравнения, принадлежащие отрезку
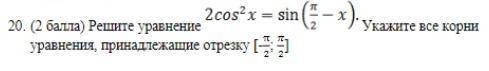
Другие вопросы по теме Математика
Популярные вопросы
- Na массой 12 г. поместили в этиловый спирт . какой объём водорода...
2 - Если в некоторой десятичной дроби перенести запятую влево на один...
2 - Как вы понимаете слова, что коста 《подерживал в них (собаках) веру...
1 - Что больше 2дм3см или 3дм 2см / 1 дм 4 см или 14см...
3 - Чем отличаются климатические показатели областей умеренного пояса...
1 - Выталкивающая сила не зависит от…1)…объёма тела; 2)…плотности тела;...
2 - Периметр прямоугольного участка--288 м, длина--80 м. найди площадь...
3 - Решить : стоимость курсов иностранного языка на человека 5500р. группе...
2 - Перевести в метры3. 250дм3*3+125дм3*2...
2 - Сколько г осадка получится при взаимодействии избытка серной кислоты...
3
а) x=п/2+пk; x=+-п/3+2пk
б) -п/2; -п/3; п/3; п/2
Пошаговое объяснение:
По формуле приведения: 2cos^{2}x=cosx
Всё в левую сторону: 2cos^{2}x-cosx=0
cosx за скобку: cosx(2cosx-1)=0
Произведение = 0, когда хотя бы один из множителей = 0, поэтому приравниваем каждый множитель к 0:
cosx=0
x=п/2+пk
2cosx-1=0
cosx=1/2
x=+-п/3+2пk
Корни, принадлежащие промежутку: -п/2; -п/3; п/3; п/2