1. Математика
  2. Решить уравнение [tex]x+\sqrt{17-x^{2}

Решить уравнение
x+\sqrt{17-x^{2} } +x\sqrt{17-x^{2}} =9

Oven463 Oven463    1   26.12.2019 13:55    4

Ответы
Rusynyk Rusynyk  23.08.2020 12:03

Умножим обе части уравнения на 2: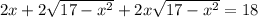 2x+2\sqrt{17-x^{2}}+2x\sqrt{17-x^{2}}=18; Теперь рассмотрим выражение

(\sqrt{17-x^{2}}+x)^{2}=17+2x\sqrt{17-x^{2}}; То есть почти то, что мы имели. Будем "достраивать". С учетом вышеизложенного замечания уравнение примет вид (\sqrt{17-x^{2}}+x)^{2}+2(x+\sqrt{17-x^{2}})+1=36;

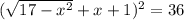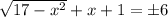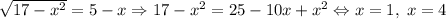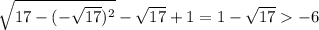Слева - квадрат суммы: (\sqrt{17-x^{2}}+x+1)^{2}=36; Итак, \sqrt{17-x^{2}}+x+1=\pm 6; Рассмотрим случай с +6: \sqrt{17-x^{2}}=5-x\Rightarrow 17-x^{2}=25-10x+x^{2} \Leftrightarrow x=1,\; x=4. Проверяем эти корни - подходят. С -6 можно не проверять: минимум рассматриваемой функции равен \sqrt{17-(-\sqrt{17})^{2}}-\sqrt{17}+1=1-\sqrt{17}-6;

ответ: 1, 4

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
kennY1771 kennY1771  14.10.2019 15:27
Найди сумму трех слагаемых, если первое слагаемое 100, второе на 100 меньше первого слагаемого, а третье на 100 больше второго слагаемого. с подробным !...
Кролик1922 Кролик1922  14.10.2019 15:27
Выполните 1 делимое - 36, делитель - 8, сосны минут 4 найдите остаток 2 сумма 3 последовательных чисел равна 21 найдите эти числа 3 чему равен наименьший делитель если...
lisnyakmashenk lisnyakmashenk  14.10.2019 15:27
34 сделайте 7 и 8 с решением вроде легкие, но у меня не получается сделать....
zizi131 zizi131  14.10.2019 15:27
Расстоянте от деревни до леса-5 км.это в 3 раза меньше чем от леса до озера.сколько километров от деревни до озера? ​...
vikhas123 vikhas123  14.10.2019 15:29
Сократите обыкновенные дроби.* 1) 5/15 2) 10/35 3) 6/18 4) 14/49 5) 16/40 6) 100/200 *, *...
gosharybchinckyi gosharybchinckyi  14.10.2019 15:29
проверь, составляет ли пропорции отношения. а) 41: 0,2 и 738: 3,6...
Алекс117829 Алекс117829  14.10.2019 15:30
Существует ли 19 значное число у которого сумма цифр равна произведению цифр? ​...
gnikitav2007 gnikitav2007  14.10.2019 15:30
Магазин продал за три дня 600 кг картофеля в первый день продали 180 кг а остальное продали во второй и третий день поровну вопрос краткая запись...
hahahagall hahahagall  14.10.2019 15:30
От разности чисел 60и 10 отнять 30...
ренатик9 ренатик9  14.10.2019 15:31
Будь ласка, іть із 1, 3 та 4 завданнями ​...

Популярные вопросы