решить уравнение по комбинаторики
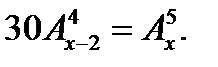
Другие вопросы по теме Математика
Популярные вопросы
- Скаким современеными производствами ассоциируются название отдельных городов?...
3 - Утайзi тварини добре пристосувалися до...
3 - Проанализируйте и поразмышляйте о маленькой трагедии а.с. пушкина ( 34 ! )...
3 - Составить предложения со словом party...
3 - Всё было усыпано пахучими лепестками жасмина. - сделать синтаксический разбор предложения...
2 - Какой стебель у яблони? особые интересные факты о стебле яблони и его функции...
1 - Решите систему уравнений: {х-2у=8 {х-5у=6...
2 - Write the same in english. 1)полчаса; 2)полтора часа; 3)пол-яблока; 4)полтора банана;...
1 - Олшемге катысты создин: 1кылдай,2иненин козиндей,3тырнактай,4оймактай,5бир ели,6бир...
1 - Удвох пакетах 42 кг цукерок. у другому пакеті у 5 разів більше цукерок, ніж у першому....
1
x1=6, x2=25
Пошаговое объяснение:
так как A(m, n)=n!/(n-m)!, где 0!=1, 1!=1, 2!=1*2=2, 3!=1*2*3=6, ... , n!=1*2*...*(n-1)*n
то 30*А(4, х-2)=А(5, х)
30*(x-2)! / (x-2-4)! = x! / (x-5)!
30*(x-2)! / (x-6)! = x! / (x-5)!
Домножим обе части уравнения на (x-5)! / (x-2)!
(Отметим, что x!=(x-2)!*(x-1)*x, (x-5)!=(x-6)!*(x-5))
30*(x-5) = (x-1) * x
30x-150=x^2-x
x^2-31x+150=0
D=(-31)*(-31)-4*1*150=961-600=361=(19)^2
x1=(-(-31)+19)/(2*1)=50/2=25
x2=(-(-31)-19)/(2*1)=12/2=6