Решить уравнение log1/2(x2-5x+6)=1
Другие вопросы по теме Математика
Популярные вопросы
- Сочинение на тему как я провел лето что мне запомнилось? что изменило мои...
1 - Задумали число увеличили его на 60 результат уменьшили на 76 получили 78...
1 - Напишите сообщение «что такое слово? лексическое значение слова»...
3 - Найдите произведение чисел: а) 0,1 и 10; б) 0,1 и 1000; в) 0,01 и 10; г)...
3 - Вычисли площадь пола классной комноте (в классе ширина 6м длина 12м)...
1 - На завтра нужно: доказать что существует натуральное число последние четыре...
3 - Длина цветка 18, 84 метр. найдите площадь цветка....
3 - Найдите значение выражения: 70-(10,2-3,38) x 4,4+10,008...
1 - татьяна тесс голубой ель зжатое изложение надо...
1 - На складе работают 5 рабочих. двое из них зарабатывают в месоц по 6900 крон,двое...
2
ответ: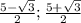
Пошаговое объяснение:
ОДЗ:
С учётом ОДЗ оба корня подходят.