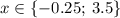решить уравнение,если можно по действиям

Другие вопросы по теме Математика
Популярные вопросы
- Составьте рассказ о деятельности, используя план: — О каком человеке (своём...
2 - Упражнение 1. Замените выделенные слова на местоимения. 1. I voit son frere....
1 - Вариант 8. По результатам экспериментов были получены сле-дующие показатели...
2 - Это не по школе как изменить ник?...
2 - Взяв 7 конфет, Илья взял 1/3 часть всех конфет, что были в вазе. Сколько конфет...
3 - 1. Жырдағы Кенесары образын І.Есенберлиннің «Көшпенділер» трилогиясындағы Кенесары...
1 - Вычислите количество тепла (кДж), выделяющееся при образова-нии из простых...
1 - Ла ы у т о и н что делать задание 1 класс...
3 - Определите аккорды в приведённых ниже примерах:...
2 - Доповніть схему Хрещення Русі-України ....
2
Пошаговое объяснение:
Данное решение предполагает, что при вычислении логарифма
сначала возводим (х-1) в 4 степень, и лишь потом вычисляем логарифм, учитывая что значение под логарифмом должно быть больше 0
ОДЗ:
Очевидно, что знаменатель не может быть равен 0, поэтому раскроем можуль следующим образом:
х = 3,5 является корнем уравнения
х = -0,25 тоже является корнем уравнения
ответ: