Решить уравнение cos0,2x-cos0,8x+cos0,6x=1 , !

Совокупность:

x=π/0,8+(πk/0,4), k∈N;

x=-π/0,4+10πp, p∈N;

x=π/1,2+10πq, q∈N;

x=5π/1,2+10πm, m∈N.

Пошаговое объяснение:

cosa+cosb=2cos((a+b)/2)*sin((a-b)/2)

(cos0,2x+cos0,6x)-cos0,8x=1

2cos0,4xsin0,2x-cos(2*0,4x)=1

Вычитаемое раскладываем по формуле двойного угла (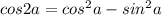), единицу заменяем на тригонометрическое тождество и переносим влево.

cos0,4x=0, 0,4x=π/2+πk, x=π/0,8+(πk/0,4), k∈N;

или

Решаем квадратное уравнение относительно sin0,2x.

По теореме Виета:

sin0,2x=-1, 0,2x=-π/2+2πp, x=-π/0,4+10πp, p∈N;

или

sin0,2x=1/2, 0,2x=π/6+2πq или 0,2x=5π/6+2πm, x=π/1,2+10πq или x=5π/1,2+10πm.