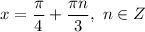решить уравнение 2sin^2(2x)=(cosx+sinx)^2
Другие вопросы по теме Математика
Популярные вопросы
- Велосипедист едет со скоростью 15 км в час по пологой дороге....
3 - , Камиля испекла круглый торт и разделила его на 3 части (сектора)....
2 - заранее Церковная реформа Патриарху Никона сравниваем, размышляет...
2 - Яке поняття зайве у рядку монополія трест картель протекціонізм...
1 - БАЛІВ. ЗРОБІТЬ ТЕ, ЩО Я ВИДІЛИВ В ПРЯМОКУТНИК, ТРИ ЗАВДАННЯ! ДЯКУЮ......
1 - Ученик прочитал в понедельник 2/5 всей книги,во вторник 1/2 оставшихся...
1 - Какое число повторяется слогаемым в произведении 56×30...
2 - Установіть відповідність між рослинамі та іх відділамі до яких...
3 - Rewrite the sentences. Put the words in brackets in the correct...
2 - У трикутнику АВС точки К і L - точки дотику сторони АВ до вписаного...
3
Замена: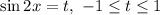
Получили три ответа с наименьшим положительным периодом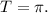
На единичной окружности найдем объединение всех ответов. Заметим, что все три ответа повторяются через треть окружности (см. рисунок), поэтому: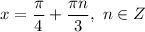
ответ: