Решить уравнение:
2 (2cos4x + 1) · cosx = 1
Другие вопросы по теме Математика
Популярные вопросы
- Установие соотвествие: 1. Водоупорные породы А.Песок 2.Водопроницаемые...
2 - ответ надо очень пабыстрей...
1 - ОТВЕТИТЬ НА ВО И 13 ПОЛЬЗУЯСЬ ТЕКСТОМ. НА ОСТАЛЬНЫЕ Я ОТВЕТИЛА...
1 - На U и оп7. Площадь территории России 17 075 тысяч кв. км, Казахстана -...
2 - Весной в Центральной России в г. Смоленске установилась холодная дождливая...
1 - В триугольнике ABC отрезок BD - медиана. AC = 10 см. найдите длину отрезка...
2 - Реальный ВВП базисного года составляет 1400 ден. ед. За текущий год реальный...
1 - Роль Коммунистической партии в Советском Союзе! Чем функции Коммунистической...
1 - Между Римом и Карфагеном в 221 г.до н.э. был заключен мировой договор....
3 - Кого переміг князь Володимир Великий?...
1
Пошаговое объяснение:
Так как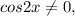 то
то
Так как должны выполняться условия :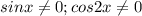 , то
, то