Решить уравнение #18 и #19

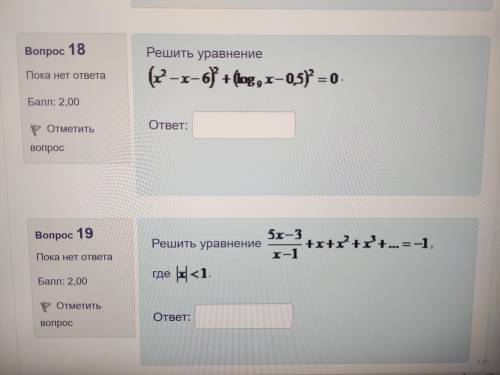
18. Поскольку и 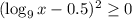, левая часть может равняться 0 только тогда, когда оба квадрата одновременно равны 0, т.е. нужно решить систему

Решим второе уравнение:

Т.к. число 3 является корнем первого уравнения,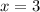 - решение системы и решение исходного уравнения. Других решений оно не имеет.

19. Упростим сумму (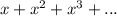). При 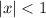она представляет из себя сумму членов бесконечно убывающей геометрической прогрессии  с первым членом 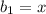и знаменателем 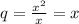. По формуле 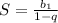запишем сумму:

.

Перепишем исходное уравнение в виде

.

18. Сумма квадратов двух выражений равна нулю когда оба выражения равны нулю. Кроме этого ㏒₉х определен, когда х>0,

х²-х-6=0 имеет корни по Виету х=3, х=-2, второй корень не входит в ОДЗ уравнения.  ㏒₉х-0.5=0, ㏒₉х=0.5; х=9⁰.⁵=3

ответ 3

19.  х+х²+х³+...=х/(1-х) по формуле суммы бесконечно убывающей геометрической прогрессии. s=b₁/(1-q) . где b₁=x: q=x²/x=x³/x²=x

(5х-3)/(х-1)+х/(1-х)=-1; х≠1; (5х-3-х)/(х-1)+1=0;  4х-3+х-1=0; 5х=4; х=4/5-ответ попадает в заданный промежуток (-1;1)

ответ 4/5