Решить тригонометрическое уравнение с подробным объяснением. 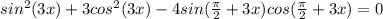
Другие вопросы по теме Математика
Популярные вопросы
- Когда была куплена аляска? в чем главный смысл и определяющая роль этой сделки?...
3 - Замени дробь равной ей дробью со знаменателем 24 а) 3/8 б)5/6 ....
2 - Кратко опишите ситуацию во франции в месяцы якобинской диктатуры . выделите...
1 - Составь выражение и найди его значение саша наклеил в альбом 30 марок что составляет...
2 - Проверочное слово к слову преподаватель на букву о...
1 - Из пункта а в направлении пункта в вышел турист со скоростью семь целых одна...
1 - Каких перепончатых человек использует в биологической борьбе с насекомыми...
2 - Начерти в тетради квадрат в масштабе 1 см-1 м со сторонами 3 м...
1 - Напишите эссе(ну или сочинение) о том, чему нас учат произведения пушкина?...
2 - Какая тектоническая структура у эфиопского нагорья?...
2
1случай.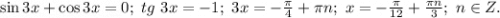
2 случай.
В ответе нужно записать обе серии.