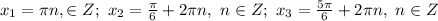Решить тригонометрическое уравнение
Другие вопросы по теме Математика
Популярные вопросы
- 1.Почему «великолепная панорама» города кажется Раскольникову холодной? 2....
3 - ЖАЗЫЛЫМ-тапсырма.«Ассоциограмма». Компьютерге қатыстыөзің білетін сөздерді...
3 - Характер и внешний вид (описание ) словами автора текста Белолобый ...
2 - Составте рассказ о значении потребностей в жизни человека ,используя сл дущий...
1 - Очень надо! ABCD-квадрат, МО-перпендикуляр к плоскости ABC,......
3 - Равнобедренный треугольник, у которого периметр равен 28 см, а по бокам и...
1 - Илашение :КолишнееagaraDano:P1 =9864all- 120 иa h= 12 M кк? ...
1 - МАШНЕЕ ЗАДАНИЕДОМАШРеши задачу.10азин привезли 90 дыньопи 2 части привезённыхСколько...
3 - Решите пример (0,7х-0,6у+0,5z)•(-1,5p)=...
3 - 1084. Координаталық жазықтықта:1) y=0; -2 x 5; - 3) y=2; -1 x 4./2) x=0; -2...
1
В левой части уравнения применим неравенство Коши
Поэтому это равенство возможно, когда
для удобства сделаем замену:
также:
получим:
подбираем корни:
используем схему горнера:(см. вложение)
Получим:
Используем формулу Кардано:
уравнение вида
ax^3+bx^2+cx+d=0
с замены
приводим к виду
где:
Для данного уравнения(для удобства a заменим на x):
Определим величину Q:
Q>0 => уравнение имеет один действительный и два комплексно-сопряженных корня
Ищем только действительный корень:
В итоге:
обратная замена:
ответ: