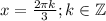решить тригонометрические уравнения.
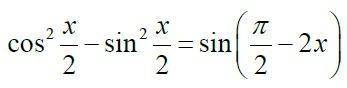
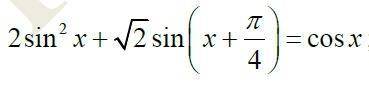
Другие вопросы по теме Математика
Популярные вопросы
- Рассказ на тему : воображаемое путешествие по реке клязьма...
3 - Одинакова ли предельная полезность купюры в 100 долларов сша для преподавателя...
3 - Расстояние от метеорологической станции до избушки лесника-18 км....
1 - 14.17*заполните пропуски притяжательными местоимениями в абсолютной...
1 - Решите : 1. мастер сплёл больших корзин на 15 штук больше, чем маленьких...
1 - Рассказать на про пушкинский музей- какие картины зарубежных художников...
2 - Перевести ! it’s eleven o’clock in the morning. helen petrova’s in...
1 - При пересечении двух прямых один из полученых углов равен 1)75; 2)120.найдите...
2 - Make questions for these answers. 1) during their holidays they got...
3 - Как и почему меняется роль на международной арене в 30 годы...
1
Cерия решений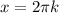 присутствует в серии решений
присутствует в серии решений  , значит в ответ запишем одну серию.
, значит в ответ запишем одну серию.
ответ: