Решить тригонометрические неравенства,
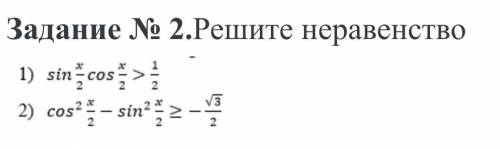
Другие вопросы по теме Математика
Популярные вопросы
- В наших краях лучшие арбузы из Каракумов. Встречаются арбузы тяжелее...
1 - Выделить черты сталинизма-тоталитаризма и сделать вывод! Накину ещё...
3 - Халявные (нет) Отгадайте загадку : Кто сначала ходит четырьмя ногами...
2 - Желательно с рисунком ответ...
2 - Напишіть рівняння реакції в нейтралізації,якщо в результаті утворюється...
2 - ЗАРАНИЕ Сказки о Шише» Б.В. Щергина как литературные сказки Проанализируйте...
1 - За 3 кг апельсинів і 4 кг бананів заплатили 150 грн. Скільки коштує...
3 - 2 Don t forget to ... pictures at thewedding, Marisa is going to...
3 - 4. Из (5) предложения выписать слово в котором есть суффикс-Л-....
2 - 8 | Какие из утверждений верны?На Сенатской площади представители...
2
1.
умножим на 2
это формула двойного угла:
область определения синуса:
следовательно неравенство не имеет решения.
2.
это формула двойного угла:
рисунок
n принадлежит Z.