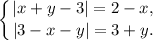решить систему уравнений (желательно с подробным решением)
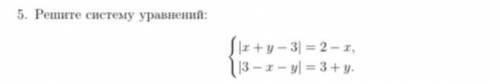
Другие вопросы по теме Математика
Популярные вопросы
- автомобиль двигался со скоростью 128 км/ч и путь 12 км. какое время...
2 - 2. Яка з перелічених властивостей характерна тільки для аморфних тіл?...
3 - Вот все, что надо сделать Даю 100 б. за правильный ответ....
2 - Сделай синтаксический разбор простого предложения (подчеркни все имеющиеся...
2 - написать выводы к таблице по Химии. Тема: Решение экспериментальных...
2 - ГРУППА 6 ГЛ. 7 СТР. XXXII-XXXVII Вопросы: 1. Тема и центральная проблема....
3 - Скласти двоскладне та безособове речення зі словом бажати...
2 - , заранее 5 проблем на территории РФ техногенного характера...
1 - Дано треугольник ABC BC=15 AC=18 угол B = 40 градусов Найти угол А...
2 - какую массу спирта потребуется чтобы лёд массой 300 г при температуре...
2
(-2; 1)
Пошаговое объяснение:
Заметим, что x + y - 3 = -(3 - x - y), то есть подмодульные выражения — это противоположные числа. Если один модуль раскрывается с плюсом, то другой — с минусом.
Пусть x + y - 3 ≥ 0:
6 - 7 - 3 = -4 < 0, что не удовлетворяет условию x + y - 3 ≥ 0. Значит, данное решение не подходит.
Пусть x + y - 3 < 0:
-2 + 1 - 3 = -4 < 0, условие выполняется, значит, данное решение подходит.
Решите систему уравнений: