Решить систему 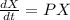$\frac{dX}{dt} =PX$ линейных однородных уравнений с постоянными коэффициентами ( 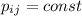$p_{ij} =const$ ) при заданных начальных условиях, если $P=\left[\begin{array}{ccc}p_{11} &p_{12} &p_{13} \\p_{21} &p_{22} &p_{23} \\p_{31} &p_{32} &p_{33} \end{array}\right]; X=\left[\begin{array}{c}x(t)&y(t)&z(t)\end{array}\right]; \frac{dX}{dt}=\left[\begin{array}{c}x'(t)&y'(t)&z'(t)\end{array}\right]; X_{0}=\left[\begin{array}{c}x(0)&y(0)&z(0)\end{array}\right]; P=\left[\begin{array}{ccc}3&-3&4\\6&9&-1\\5&3&4\end{array}\right]; X_{0}=\left[\begin{array}{c}3&7&9\end{array}\right]$

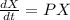
Решить систему линейных однородных уравнений с постоянными коэффициентами () при заданных начальны

Ответы

Показать ответы (3)

Другие вопросы по теме Математика

матвей100000001357 06.09.2021 22:36

whiteandblackca 06.09.2021 22:36

Знайти область визначення функції...

karolsevilla384 06.09.2021 22:36

ТарасБульба1 06.09.2021 22:36

, по действиям, с подробной записью•́ ‿ ,•̀...

aleks1yus 06.09.2021 22:35

Пиирмвп 06.09.2021 22:35

Тендеу памогете 6 класс(1,75+x) : 1,9=12-9,5...

Evgenia111111111111 06.09.2021 22:35

кроп1 06.09.2021 22:35

Решите пример . Это один единый пример...

kolomietslina 06.09.2021 22:35

anton270 06.09.2021 22:34

Решить систему линейных однородных уравнений с постоянными коэффициентами () при заданных начальных условиях, если