решить систему дифференциальных уравнений . Ничего не получается у меня . Прикрепляю фото
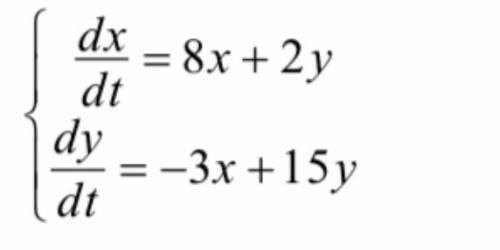
Другие вопросы по теме Математика
Популярные вопросы
- 1. Как распределены звездные скопления в галактике? 2. Почему светятся...
2 - Почему Александр медонский ответил именно так? О чем идет речь в отрывке?...
2 - Зробіть будь ласка максимально балів...
2 - Отрицательные качества героев из произведения Бедность не порок ...
3 - Складіть рівняння хімічних реакцій, які відповідають схемам послідовних...
1 - Если на заводе по производству анилина из 41 т нитробензола удаётся...
1 - Прочитайте. Найдите и выпишите из текста слова, заполните таблицу: Иван...
3 - нужна транскрипция как читается на русском языке немецкий:Ihr,Kinder,heraus!...
2 - Put the verbs in brackets into Present Perfect or Present Perfect Continious...
3 - 1 из 2Тест по теме « Революция 1917 года ».1. Что из перечисленного...
2
подставляем (1) и (2) в (3)
получаем:
подставляем (.) и (..) в (...)