Решить sinx+cosx=1 с подробным решением. заранее
Ответы
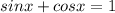
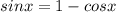
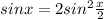
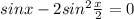
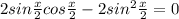

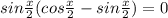
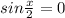 или
или 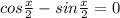
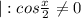
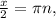
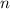 ∈
∈ 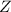 или
или 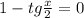
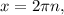
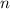 ∈
∈ 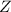 или
или 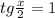
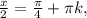
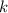 ∈
∈ 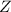
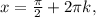
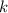 ∈
∈ 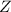
Другие вопросы по теме Математика
Популярные вопросы
- Выражение (5a( в 2 степени) b) ( и это все во 2 степени ) ! 1...
1 - Вряду два узора сделаны из желтых ниток.в одном из узоров 8 желтых...
2 - Уучителя было 36 тетрадей.он раздался 2 ученикам по 4 тетради.сколько...
2 - 7класс, : найдите стороны ровнобедренного треугольника, если его...
2 - Составь выражения: 4×8 □÷□ используя таблицу умножения, вычисли...
3 - Сделать фонетический разбор слова часов надо...
3 - Напишите 3 слова с буквы безударных гласных в приставках...
2 - Укажите названия госурдств с которыми граничила россия до 1533...
3 - На лево на право я вас направляю .машинам автобусу путь выбираю.себе...
1 - Всавить числа в пирамиду первый этаж известно 2 и два окошка пустых,...
2