решить самостоятельную по теме "Производная сложной функции" как можно быстрее
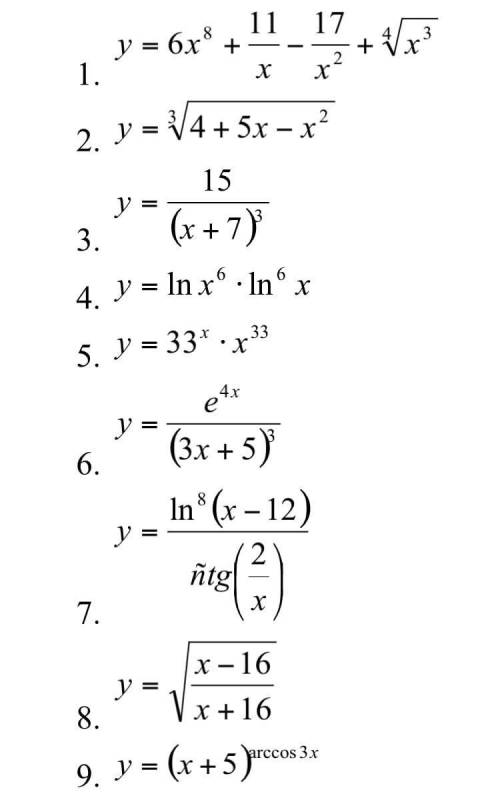
Другие вопросы по теме Математика
Популярные вопросы
- Составьте предложения с выделенными словами мы долго искали ключ. завод работает...
1 - )) два поезда шли с одинаковой скоростью.один был в пути 7ч.,другой-5ч.первый...
1 - Придумать сказку про носок,шапку и варежки(не большая)...
3 - Скільки витків повинна мати котушка площею поперечного перерізу 50 см^2, щоб...
1 - Why you come late yesterday? a) does; b) do; c) did; d) is; e) are; 2. my friend...
3 - Велосипедист проехал 45 км за полтора часа. сколько времени потребуется велосипедисту...
2 - Составьте уровнение реакций горения для серы 4 валентный...
1 - Во рту маковой росинки не было.слово из 5 букв.из сказки джельсрмино в стране...
2 - Составьте смеху предложения. кто-то из старших мальчишек мне рассказал: ,,если...
2 - Определить стоимость потреблённой электро энергии, если в начале месяца счётчик...
3
по формуле: