РЕШИТЬ РАЦИОНАЛЬНОЕ НЕРАВЕНСТВО
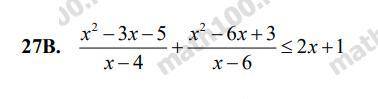
Другие вопросы по теме Математика
Популярные вопросы
- План описания маршрута: 1. Указанные маршруты описываются в виде...
3 - вроде так, но не принимает...
1 - Здравствуй. Ты можешь изучить тему сегодняшнего урока, используя...
3 - Распределите слова по орфограммам а)чередующаяся гласная в корне...
2 - написать письмо Печкину меняя разные связи предложений. Заранее...
2 - ОБРАЗУЙТЕ ФОРМЫ СРАВНИТЕЛЬНОЙ СТЕПЕНИ ПРИЛАГАТЕЛЬНЫХ. ОТ КАКОГО...
1 - Лесу, плыть по морю, выращивать на поле, посадить в саду, Твительных...
2 - Странице 105, приВычитании,как317. Прочитай набой числаСВязаныимеждузаполни...
1 - (1/a:1/2b:4c+3/2ac)*2ac/b+3 Упростите выражение...
3 - ОБРАЗУЙТЕ ФОРМЫ СРАВНИТЕЛЬНОЙ СТЕПЕНИ ПРИЛАГАТЕЛЬНЫХ. ОТ КАКОГО...
2
(-∞; 3] ∪ ( 4; 6) .
Пошаговое объяснение:
Нанесем на числовую прямую точки нули знаменателя: 4 и 6 и нули числителя
И определим знак и получим
х∈ (-∞; 3] ∪ ( 4; 6) .