Решить производную функции: y=arcsin(log3x)
Ответы
Находим производную от сложной функции: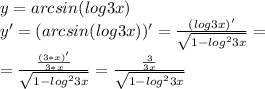
ПОКАЗАТЬ ОТВЕТЫ
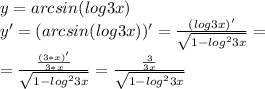

Другие вопросы по теме Математика
Популярные вопросы
- Where s mummy? she s in the g закончить предложение...
1 - Длинна участка прямоугольной формы 9 м.найди перипетр участка...
3 - Іть визначити морфеми (закінчення, корінь, префікс , суфікс,...
2 - Нужна ! такое: с двумя причастиями поставьте 2 предложения с...
2 - 8. усі дієприслівники з часткою не пишуться окремо в рядку: а)...
2 - A1чему равна сумма внутренних углов выпуклого n-угольника 1)180°⋅(n-2)...
3 - Решипример вставь числа 88000**90)87+(60-20)=...
3 - Какое количество керосина необходимо сжечь, чтобы 50 л воды нагреть...
3 - Составте предложения из этих слов 1)doesn t 2)parties 3)my 4)...
3 - Магазин получил 156 пар детской обуви, 165 пар мужской обуви,...
3