решить. Пробовала по-разному, но какая-то билиберда получается
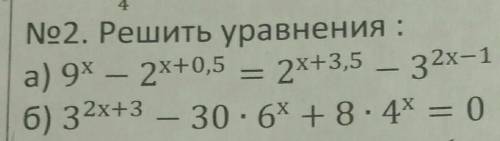
Другие вопросы по теме Математика
Популярные вопросы
- Как оброзовалось слово издавна...
3 - Сходства и различия двух монархов: Императора Токугава в Японии...
2 - До іть виконати 3 завдання(потрібно зараз)...
1 - Определите какая жидкость налита в ёмкость высотой 80см ,если...
1 - Чем по мнению автроа отличается город от деревни в повести пахарь...
3 - У трикутнику АВС АВ = СВ. Бісектриса кута В перетинає сторону...
2 - РАСКРЫТЬ СМЫСЛ ЭТОЙ ФРАЗЫ ОБЪЁМ НЕ МЕНЕЕ 150 Слов! «Если вы станете...
3 - На продовженні медіами BM трикутнтка ABC позначеного точку так,...
2 - CD / a / a / went / new / or / shop / Then / music / we / to поставити...
2 - Определите степень одночлена –12,79....
2
а)Перепишем так
9^x*(2/3)=2^(2x+3,5)
9^x=3*2^(2x+2,5)
3^(2x-1)=2^(2x-1+3,5)
(3/2)^(2x-1)=8*sqrt(2)
2x-1=log(3/2) (2^3,5)
2x-1=3,5*log(3/2)(2)
x=0,5+1,75**log(3/2)(2)
Можно написать поизящней, но логарифм останется.
б)
3^x=a 2^x=b
9*a^2-30ab+8*b^2=0
9*a^2-30ab+25*b^2=17b^2
(3a-5b)^2=17b^2
1) 3a-5b=sqrt(17)b
3(a/b)=5+sqrt(17)
(a/b)=(5/3)+sqrt(17)/3
(1,5)^x=(5/3)+sqrt(17)/3
x1=log(1,5)((5/3)+sqrt(17)/3)
2) 3a-5b=-sqrt(17)b
(a/b)=(5/3)-sqrt(17)/3
x2=log(1,5)((5/3)-sqrt(17)/3)
Оба решения годятся, т.к 5 больше корня из 17
Решения не красивые, но, кажется, такие числа.