решить :
Нужно решить неопределенное интегралы
штук 5-7 на выбор
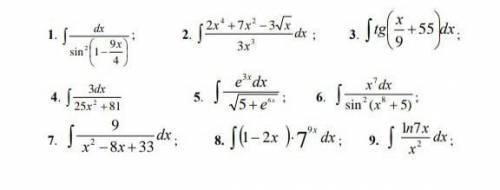
Другие вопросы по теме Математика
Популярные вопросы
- Выберите верные утверждения. 1)По численности населения район уступает...
3 - Составить и записать план рассказа и 3 во по тексту,, Тринадцать...
3 - Позначте формулу сполуки що не належить до основ 1.LiOH 2.Al(OH3)...
2 - Наружная оболочка глазного яблока 1 Стекловидное тело 2 Склера 3...
2 - Планеиа противоположное слово...
3 - Які риси характеру властиві Прометею?...
3 - Найди в этом тексте 5 прилагательных в превосходной форме. ...
3 - Превратите предложения в отрицательные и переведите. 1.Ann was bitten...
3 - Кто герои рассказа или произвеления...
2 - Для агроэкосистем и естественных экосистем характерно наличие: 1)...
3
1.
2.
3.
4.
5.
6.
7.
8.
Решаем по частям:
9.
По частям: