Решить несобственные интервалы
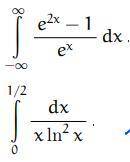
Другие вопросы по теме Математика
Популярные вопросы
- Казакстан галымдар» такырыбына биылгы жылы мерейтойы болатын корнекты...
2 - Пэрший члэн арыфмэтичной прогрэсии доривнюе -4, а йи ризныця доривнюе...
2 - Почему можно и матрац, и матрас? Если знаете напишите почему можно...
1 - Чи завжди серед будь-яких цілих 6 чисел, знайдеться 2 числа, різниця...
1 - Сделать по таблице брадиса 8 с переносом запятой...
2 - 2-тапсырма. Сұрақтарға жауап беріңдер. 1. Ғарыштық денелер дегеніміз...
3 - 6. Знайдіть п ятий член геометричної прогресії (b), якщо b = 3,4...
2 - написати r, x, p, що характерезують хімічні властивості ...
3 - В одной корзинке 11_3 кг яблок, что на 1 кг больше, чем во второй....
1 - Вставить пропущенное окончание (доказать двумя ) ПОГАСиТЕ, СТАВиТЕ,...
2
Пошаговое объяснение:
1)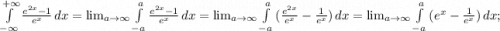
2)