решить неравенство и понять где ошибка в моем решении Верный ответ под цифрой 2.

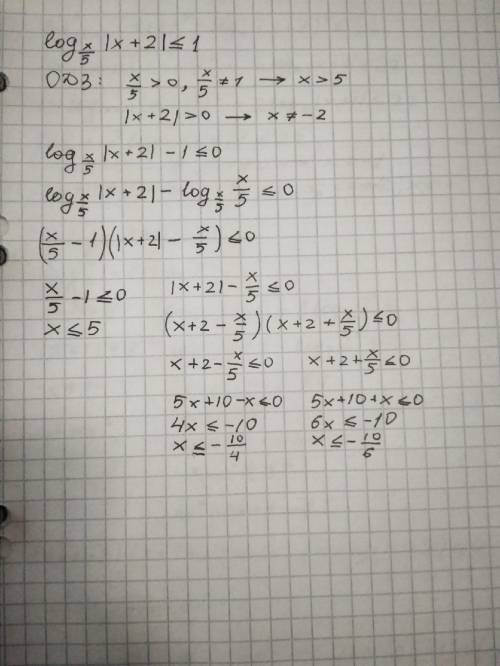
Другие вопросы по теме Математика
Популярные вопросы
- Лабароторная работа в файле это...
3 - Установіть послідовність у схемі одержання брометану 1) CH4 2)...
3 - Решите привести подобные члены . 38у4+12у4-85у4 даю 10б...
1 - Задание 3. Верно - неверно (отметьте утверждения): 1) на территории...
2 - Укажите вид сказуемого в предложении: Я буду сильно беспокоиться....
1 - сделайте АНАЛИЗ любого стихотворения Михаила Михайловича Люгарина,...
2 - Приріст прибутку за 2 варіантом капіталовкладень , тис . грн....
3 - 1. На урок математики принесли коробку с кубиками. Рассмотр рисунок...
1 - Первая медицинская если натёр ногу (по пунктам) ...
2 - НАПИШИТЕ СОЧИНЕНИЕ ЗАВТРА ПИСАТЬ написать сочинение описание памятника...
2
Пошаговое объяснение:
Решение задания приложено
В вашем решении есть две критические ошибки
1-я, это когда вы получили x>5
2-я это в момент перехода от неравенства ab<=0 к неравенствам a<=0 и b<=0
Исходя из того, что Вы используете метод замены множителя, или метод рационализации, понятно, что изучаете углубленку.
Теперь об ошибках.
1. из того что (х/5)>0 ⇒x>0, достаточно обе части умножить на пять. знак останется прежним.
2. из того, что (х/5)≠1, следует, что х≠5, опять же умножьте обе части на 5.
3. ((х/5)-1)(Ix+2I-(x/5))≤0 Я бы решал методом интервалов. Но если Вы избрали иной путь, то опять же должны рассмотреть случаи, когда знаки у множителей различны, т.е. первый ≥0, второй отрицат., и наоборот, первый ≤0, а второй положит. Вы же разобрали случай, когда оба множители неположительны.
Ну, и теперь решение.
Помня, что метод рационализации срабатывает на ОДЗ, еще раз подчеркнем ее, х≠-2 мы не учитываем, т.к. пересечением трех условий х≠-2; х∈(0;5)∪(5;+∞) является х∈(0;5)∪(5;+∞)
Рассмотрим ((х/5)-1)(Ix+2I-(x/5))≤0 на ОДЗ;
((х/5)-1)(Ix+2I-(x/5))≤0 можно переписать так :
((х/5)-1)(x+2-x/5)≤0 , домножим обе части на 25=5*5, получим (х-5)(4х+10)≤0, решим методом интервалов.
___-2.55
+ - +
решением неравенства является х∈[-2.5;5], учитав ОДЗ, получим ответ
(0;5) , в этом интервале целыми решениями будут 1;2;3;4, а их сумма равна 1+2+3+4=10
ответ 10
ЧТО ОСТАЛОСЬ НЕ ЯСНЫМ?