1. Математика
  2. Решить неопределенный

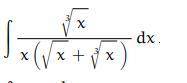
Решить неопределенный интеграл


Решить неопределенный интеграл

PeaceDuck1337 PeaceDuck1337    3   08.01.2021 21:33    0

Ответы
Пензик Пензик  07.02.2021 21:35

Пошаговое объяснение: =∫ dx/(√x+∛x)·∛x²= ∫ dx/⁶√x⁷(1+1/⁶√x)= |пусть 1+1/⁶√x=t, тогда dt/dx= -1/6 ·⁶√x⁷; dx= -6 ·⁶√x⁷·dt| = -6·∫dt/t= -6·lnt=   -6·ln(1+1/⁶√x)+C

ПОКАЗАТЬ ОТВЕТЫ
helenawoy helenawoy  07.02.2021 21:35

\int\limits \frac{ \sqrt[3]{x} }{x( \sqrt{x} + \sqrt[3]{x} )} dx = \int\limits \frac{ {x}^{ \frac{1}{3} } }{x( {x}^{ \frac{1}{2} } + {x}^{ \frac{1}{3} } )} dx \\

у переменных степени 1, 1/2 и 1/3, и их общий знаменатель - 6. Делаем замену:

{x}^{ \frac{1}{6} } = t \\ {x}^{ \frac{1}{2} } = {t}^{3} \\ {x}^{ \frac{1}{3} } = {t}^{2} \\ x = {t}^{6} \\ dx = 6 {t}^{5} dt

\int\limits \frac{ {t}^{2} }{ {t}^{6}( {t}^{2} + {t}^{3} ) } \times 6 {t}^{5} dt =6 \int\limits \frac{tdt}{{t}^{2} + {t}^{3} } = \\ = 6\int\limits \frac{tdt}{ {t}^{2} (t + 1)}= 6\int\limits \frac{dt}{ t (t + 1)}

с неопределенных коэффициентов разделим на простейшие дроби:

\frac{1}{ t (t + 1)} = \frac{A}{t} + \frac{B}{t + 1} \\ 1 = A(t + 1) +B t\\ 1 = A t + A + Bt \\ \\ 0=A+B \\ 1 = A \\ \\ A=1\\B=-1

6(\int\limits \frac{dt}{t} - \int\limits \frac{dt}{t + 1} ) = \\ = 6 ln(t) - 6 ln(t + 1) + C = 6 ln( \frac{t}{t + 1} ) + C= \\ \\ = 6 ln( \frac{ \sqrt[6]{x} }{ \sqrt[6]{x} + 1} ) + C

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
demoplus1 demoplus1  23.06.2019 01:10
Как решить ривняння 4*(2x -3)+12=96...
Kxoma Kxoma  23.06.2019 01:10
Вычесли значения каждого выражения двумя выбери самый удобный (16+12): 4...
пятимейкер пятимейкер  23.06.2019 01:10
Как отмечают масленицу в наши дни? , ....
гилеваКсения гилеваКсения  23.06.2019 01:10
4класс м.и.башмакова и м.г. нефёдова стр.36 номер 6 сама : у алёши было 1500 руб.он купил 26 батареек по 43 руб.,а затем вернул в магазин 8 неисправных батареек и получил...
сауле49 сауле49  23.06.2019 01:10
Каким действием решить пример 81+(50-31)-23...
victorastrakhan1 victorastrakhan1  23.06.2019 01:10
Площадь первого поля 16 га а площадь второго в 1 целую 1/4 раза больше. урожай пшеницы на первом поле составил 37 целых 1/2 ц с гектара, а на втором в 1 целую 2/15 раза...
Попрлекс Попрлекс  23.06.2019 01:10
Выразите в рублях и копейках: 12,01 руб; 250,09 руб...
Солі Солі  23.06.2019 01:10
Запишите в виде десятичной дроби числа: а) 3 (целых) 7/10 (дробь); 6 3/10; 11 11/100; 9 27/100; 7 9/100; 10 1/100; 1 547/1000; 13 23/1000 б) 124 4/1000; 8 12/10.000; 18...
wikwik wikwik  23.06.2019 01:10
Не выполняя вычисления, укажите выражения ,значения которых равны: а)кратны 4: 24*31; 1031*22; 917*36 .б)кратны 8: 63*56; 33*16; 17*12.в)кратны 9: 12*27*121; 13*11*18...
поать поать  23.06.2019 01:10
Построй четырёхугольник,у которого один угол прямой,один острый и два тупых....

Популярные вопросы