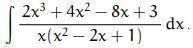
Математика: Решить неопределенный интеграл

разделим числитель на знаменатель:второй интеграл решаем с неопределенных коэффициентов:получаем:прибавляем решение первого интеграла, ответ:...

Решить неопределенный интеграл

Ответы

spl228 07.02.2021 21:22

ответ:3ln(x)+5ln(x-1) - 1/(x-1) +2x+C

Пошаговое объяснение: Выполним деление числителя на знаменатель столбиком, тогда J= ∫((8x²-10x+3)/x·(x²-2x+1) + 2)dx= ∫ (8x²-10x+3)dx/x·(x²-2x+1) + 2∫dx=∫ (8x²-10x+3)dx/x·(x-1)² + 2∫dx

Вычислим сначала первое слагаемое J₁=∫ (8x²-10x+3)dx/x·(x-1)² =

∫(3/x+ 5/(x-1) + 1/(x-1)²)dx=3∫dx/x+ 5∫dx/(x-1) + ∫dx(x-1)² =

3ln(x)+5ln(x-1) - 1/(x-1) +C ⇒ Весь интеграл: J=J₁ +2∫dx=3ln(x)+5ln(x-1) - 1/(x-1) +2x+C

ПОКАЗАТЬ ОТВЕТЫ

pavlovaalina453 07.02.2021 21:22

$\int\limits \frac{2 {x}^{3} + 4 {x}^{2} - 8x + 3}{x( {x}^{2} - 2x + 1) } dx = \\ = \int\limits \frac{2 {x}^{3} + 4 {x}^{2} - 8x + 3}{ {x}^{3} - 2 {x}^{2} + x } dx \\$

разделим числитель на знаменатель:

$\int\limits(2 + \frac{8 {x}^{2} - 10x + 3 }{x( {x}^{2} - 2x + 1)} )dx = \\ = \int\limits2dx + \int\limits \frac{8 {x}^{2} - 10x + 3 }{x {(x - 1)}^{2} } dx$

второй интеграл решаем с неопределенных коэффициентов:

$\frac{8 {x}^{2} - 10x + 3}{x {(x - 1)}^{2} } = \frac{A}{x} + \frac{B}{x - 1} + \frac{C}{ {(x - 1)}^{2} } \\ 8 {x}^{2} - 10x + 3 = A {(x - 1)}^{2} + Bx(x - 1) + Cx \\ 8 {x}^{2} - 10x + 3= A{x}^{2} - 2 Ax + A + B {x}^{2} - Bx + Cx \\ \\ 8 = A+ B \\ - 10 = - 2A - B+ C \\ 3 = A \\ \\ A = 3 \\ B = 5\\ C = 1$

получаем:

$\int\limits \frac{3dx}{x} + \int\limits \frac{5dx}{x - 1} + \int\limits \frac{dx}{ {(x - 1)}^{2} } = \\ = 3 ln(x) + 5 ln(x - 1) + \frac{ {(x - 1)}^{ - 1} }{( - 1)} + C = \\ = 3 ln(x) + 5 ln(x - 1) - \frac{1}{x - 1} + C$