Решить неопределенный интеграл
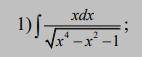
Другие вопросы по теме Математика
Популярные вопросы
- Основными ферментами в ротовой полости являются пепсин амилаза лизоцим...
1 - Якою має бути довжина прямолінійного провідника, на який у магнітному...
3 - Как необходимо поступить, чтобы защитить себя в давке в толпе?...
3 - Как конкурируют отечественные и импортные товары...
3 - У выражение 4 корень из 12+дробь 1/8 корень из 48-3 корень из 108 решите...
3 - Муз. литература 7 класс Назови музыкальные формы по буквенным схемам:...
1 - Установите соответствие между формулами исходных веществ и продуктов...
3 - Исторический диктант Соотнесите понятия и страны. Около страны поставьте...
3 - Надо поставить глаголы в нужную форму....
2 - разобраться)У меня есть дедушка , а у дедушки есть внучка тоесть дочка...
2
Выделим квадрат разности в знаменателе:
Получаем:
получили табличный интеграл: