Решить неопределённые интегралы методом подстановки.
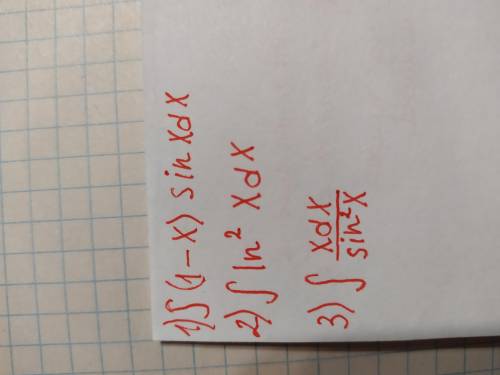
Другие вопросы по теме Математика
Популярные вопросы
- Жаттығу 34 1. Жиілігі 10^17 Гц рентген сәулесінің толқын ұзындығы...
1 - Русская Литература 6 класс.Авторы Захарова,Юстинская.Рассказ...
2 - Берілген одағай сөздермен сөйлем құраңдар.Шіркін - ай, әй, ух,...
1 - Можете написать описание на английском с переводом по этим пунктамthe...
3 - ( Решите ! Если можно письменно...
3 - Как решить такое уравнение? ( (-x+1)^-1 - (-x+4)^-1 )^2 = |x^2+6x|...
3 - Используя знание исторических фактов, объясните, почему военные...
3 - Як можа перадавацца значэнне прыблизнай колькасци? Прывядзице...
3 - решить пример по алгебре, желательно с решением и ответом 2d...
2 - Один из острых углов прямоугольного треугольника равен 60°, а...
2
Все интегралы решаются по частям.
1.
2.
3.