Решить НЕ применяя правилу Лопиталя

Другие вопросы по теме Математика
Популярные вопросы
- Решите уравнение f(x)=0, где y=f(x) - первообразная для функции...
1 - Перевести: do you remember new words frm unit 1?...
3 - Лёля нарисовала на асфальте мелом полосу из квадратиков,чтобы...
2 - План сообщение про мухомор как его составить?...
3 - Впервый магазин завезли21 мешок риса а во второй26 таких же мешков...
1 - Выделить мягкие согласные в словах пришла зима . дети рады....
1 - Найти цитату из текста описавшую васю короленко в дурном обществе...
1 - Установите последовательность этапов появления и эволюции человека,начиная...
1 - Почему выиграли шенграбенское сражение?...
3 - 5веке до нашей эры жили знаменитые греки чьи имена не забыты...
2
3.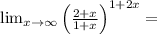
4.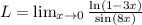
При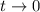
При имеем
имеем 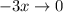 и
и  , тогда и
, тогда и