1. Математика
  2. Решить.найти работу, производимую

Решить.найти работу, производимую силой (fx, fy) вдоль дуги параболы y=x2 от точки с абсциссой x=0 до точки с абсциссой x=1.
fx=6x–3y+10, fy=10x+4y–1..
я так поняла что нужно найти интеграл по формуле\int\limits^1_0 {} (6x-3y+ dx+(10x+4y-1)dy=?

katyushamoshkop0dtz2 katyushamoshkop0dtz2    3   24.01.2020 17:30    0

Ответы
Kozlov24ivan122 Kozlov24ivan122  11.10.2020 03:00

\frac{59}{3}

Пошаговое объяснение:

Дифференциал работы - это скалярное произведение вектора силы на дифференциал перемещения:

dA=F\cdot dr=F_x dx+F_y dy

При этом мы знаем, что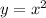 y=x^2, то есть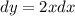 dy = 2 x dx

Итоговое выражение для работы:

A=\int_0^1(6x-3x^2+10)+2x(10x+4x^2-1) dx=\frac{59}{3}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
makarova06 makarova06  14.11.2019 16:26
Запишите координаты точек м и к, если известно что они находятся на координатной прямой на расстоянии 1 /6 единицы от точки : 1)а(5/6) ; 2) с(-2/3) ; 3)в(7/9) ; 4)р(-3/4),...
demoooon24 demoooon24  14.11.2019 16:26
Ких чито modeге11 реши, сделай проверку.714: 347 644 : 786 348 : 69688 : 16 решить 4 класс​...
sonjasonjasonja sonjasonjasonja  14.11.2019 16:26
1) 7(*) = -21; 2) -15•(*) = 60; 3) -5.(*) = -30; 4) (*)•(-4) = 36; 5) (*)•(-9) = -63; 6) (-25): (*) = -100. 16​...
наташа6710 наташа6710  14.11.2019 16:22
1. начерти в одной и той же системе координат прямые у = 3х +6,у = 3х – 9 и у = 3.2. как называется фигура, ограниченная данными прямыми и осью ох? 5. обозначь вершины...
хелпмиплиз666 хелпмиплиз666  14.11.2019 16:22
20см дин 5 тен 1 болиги 18си ден 3 тен 1 болиги 12см ден жартысы. сызып бериниздер​...
svinka03 svinka03  14.11.2019 16:21
Решите дроби на фотоответ пиши с картинкой​...
VikaDavydova2 VikaDavydova2  14.11.2019 16:21
На 50 кілометрів шляху автомобіль витрачає 3 л бензину скільки літрів бензину витратить автомобіль на 300 кілометрів шляху...
Dizzy234 Dizzy234  14.11.2019 16:20
На 50 кілометрів шляху автомобіль витрачає 3 л бензину скільки літрів бензину відтоді автомобільна 300 кілометрів шляху...
afashahbazova afashahbazova  14.11.2019 16:20
Вхоре занимаются 20 мальчиков, что составляет четыре пятых всех учащихся хора. сколько девочек в этом хоре?...
treetmeh treetmeh  14.11.2019 16:19
Решить все выполните умножение (2√a−√+b√)(3a−√2b).сократите дробь 210√−54−10√. 62√-3√−42√+3√....

Популярные вопросы